开战前炸毁三峡大坝就能打败中国?
开战前炸毁三峡大坝就能打败中国? 一、引言 这种观点不仅是对中国强大国防能力的无知,也是对三峡大坝本身战略意义和防护措施缺乏了解的表现。三峡大坝作为我国的战略级工程...
求2的平方根的三种方法
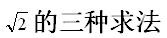
什么?还需要求的吗,不就是等于1.414(要死要死)么!
不过,我要问的是,后面呢?
呃,按个计算器不就搞定了嘛……
不过,我要问的是,计算器后面是什么呢?计算器是怎么算出
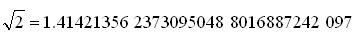
我们来介绍一下几种计算方法,数学往往是这样,看起来挺无聊的,但用于解闷倒是非常合适。
阅读本文,请准备一支笔和一个小计算器。(对自己的笔算功底非常有把握的可以不要计算器)
第一种解法,竖式计算。
先得介绍下竖式怎么算开方数。
我们可以知道,
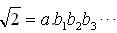
一个数一个数来凑哈。
显然,个位数应该为1,继续
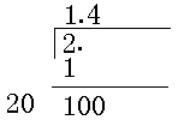
每一次补位,都是补00,两个。边上的20是第一步算出的结果1×20,其中4是不等式

的最大整数解,这是第二个准确数。

于是得到第三个准确数1。接下来同样操作即可。
为了美观,我就不对齐数位,把运算竖式写出来您可以对照下。

聪明睿智的你一定发现了,最麻烦的一元二次不等式,其实不用管那个二次项
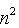
,直接估算一下就可以了。

竖式计算开方的优点是准确,通过这个方法得到的每一位都是准确值,缺点嘛……实在太慢了,即使丢掉
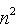
可以快速提高速度,还是很慢。
第二种解法。二分法。

来呀,拿出计算器动手试试
a
b
x
f(x)=x^2-2
b-a
1
2
1.5
0.25
1
1
1.5
1.25
-0.4375
0.5
1.25
1.5
1.375
-0.109375
0.25
1.375
1.5
1.4375
0.06640625
0.125
1.375
1.4375
1.40625
-0.022460938
0.0625
1.40625
1.4375
1.421875
0.021728516
0.03125
1.40625
1.421875
1.4140625
-0.000427246
0.015625
1.4140625
1.421875
1.41796875
0.010635376
0.0078125
1.4140625
1.41796875
1.416015625
0.00510025
0.00390625
1.4140625
1.416015625
1.415039063
0.002335548
0.001953125
1.4140625
1.415039063
1.414550781
0.000953913
0.000976563
我们发现,这个虽然很高级,但是精确度还不如竖式计算,精度设置为0.001需要10步,其准确值只有3位小数。
二分法的优点是容易理解,数学上不难,在预设误差条件下还是符合要求的。缺点嘛……不够精确,速度也不快。
第三种解法。牛顿迭代法
这个解法是这样的,先猜一个数x0,随便猜,然后代入公式
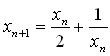
逐个计算。
拿出计算器,先动手试试比较有感觉哈。
n
x
0
4
1
2.25
2
1.569444444
3
1.421890364
4
1.414234286
5
1.414213563
6
1.414213562
只要算6次就好了,因为再算下去,结果也是一样,已经不会变了,计算器的精度用尽了。
牛顿迭代的方法优点是快,真快。我猜4已经很变态了,求2的平方根居然猜4,但速度还是超级快。缺点嘛……看不懂,真的看不懂。(呵呵)
那个迭代公式是何方神圣?我把数学过程一写您就明白了。对证明没兴趣的读者可以跳过。

当当当,公式闪亮出场!(不过,我估计您还是不懂)
但凡不懂,就先画个图,说不定就懂了。
求2的平方根,其实就是求
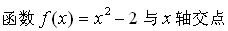
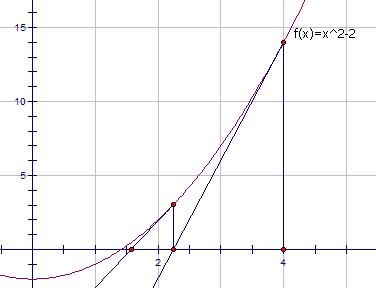
终于明白了,原来,每一次求切线与x轴交点,实际上是用切线近似地替代原来的函数,然后每一次都会与原函数的零点更接近。
其实,计算
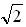
还有一个解法,也很快,叫连分数,不过这个办法只能用于一个数,而不具有推广性,我们就不介绍了。
写后记:突然有种“细思极恐”的感觉,这个问题太象高考题了。稍微变一变,比如把函数换一换就是一道现成的高考压轴题呀!

开战前炸毁三峡大坝就能打败中国? 一、引言 这种观点不仅是对中国强大国防能力的无知,也是对三峡大坝本身战略意义和防护措施缺乏了解的表现。三峡大坝作为我国的战略级工程...

1998年国足集结情况及新人名录(6):迟荣亮、王鹏、卞军、商毅 前面几篇文章对1998年国足的集训情况按时间进行了系统梳理,并介绍了国足新任主教练鲍比·霍顿和国足新人姚健、谢朝...

好电影之《和平战士》 《和平战士》一部关于觉醒题材的电影。 一位志存高远的体操运动员走向巅峰的真实事件 电影讲述了一位优秀的体操运动员--丹,在日复一日的训练中一直无法...

“宠粉”出圈的重庆:温度治理铸就城市魅力 最近,重庆这座山城在国际社交媒体上掀起了一股热潮,外国游客纷纷涌入,争相打卡。 在各大社交平台上,随处可见外国游客分享的重...

为什么二婚的很受欢迎,单身的反而无人问津? # 二婚市场的隐形困境:单身女性为何难觅良缘? 在中国婚姻市场中,一个令人困惑的现象正在显现: 尽管有数千万单身男性,许多二...

红领巾的正确系法!80后表示自己老了,网友评论亮了 在阅读此文之前,辛苦您点击一下“关注”,既方便您进行讨论和分享,又能给您带来不一样的参与感,感谢您的支持! 前言:红...

企业的组织结构 国际上通常把企业组织形式分为 独资企业、合伙企业 和 公司制企业 三大类 。 1、 独资企业 ,它是由某个人出资创办的,有很大的自由度,只要不违法,爱怎么经营就...

当年,黑枭刘汉最大的一个“保护伞”是谁?他的结局如何 在中国改革开放的历程中,涌现了众多勇于冒险的商人。他们敏锐地嗅到了机会,放弃了舒适的生活,毅然踏入商海,以智慧...

从歌手到演员和制片人 十堰姑娘许千千让梦想绽放 一路追梦的许千千。 秦楚网讯(十堰晚报) 文/记者 杨天娇 图/由受访者提供 3月19日,由十堰人许千千主演、制作并包揽影片全部原...
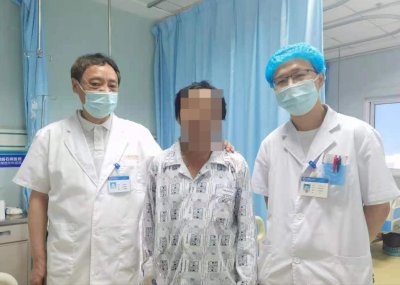
他19年前切了胆,今天却说:我太后悔了 胆囊是人体不可再生的器官,很多人在出现了胆囊息肉和胆结石的时候会选择切除胆囊。你们有过胆囊切除的体验吗?你们后悔吗? 来自毕节市...

随处可见的麻雀,曾被捕杀20亿只,现在竟是国外的“进口鸟”? 文/悠悠科普说 麻雀是一种很常见的鸟类,同时也是我们国家分布最为广泛的鸟类之一,老一辈人都知道,麻雀曾是“...

国考近5年弃考率公布,大数据推测,25年国考弃考人数可能超85万 随着2025年国家公务员考试的笔试日益临近,众多考生并未如预期那般全速冲刺于备考之路,反而萌生了退缩之意,心中...

奥黛丽赫本和纪梵希:一段跨越时空的缘分 奥黛丽赫本,一个让无数人为之倾倒的名字。她是电影史上最优雅、最迷人、最具魅力的女星之一,也是时尚界永恒的偶像。她曾经出演过《...

中华第一村,从一个贫瘠之地到全国富裕模范村,山西大寨村 这是号称中华第一村的山西大寨村,在解放以前,大寨村贫瘠的土地导致村民们常年吃不上一顿饱饭,时常发生饥荒,后来...

深圳市最漂亮的女神可能都在这里! 深圳一直都是女神聚集地,除了本地的女生天生丽质外,还因为不少外地美女们来了深圳!她们穿着时尚,风格百态不一,最重要的是一个比一个还...

15部 李沁 出演的电视剧 海上繁花 楚乔传 白鹿原 花开半夏 如懿传「2」 最近一直忙着其他的事情,也就没有更新,终于来更新啦!今天要给大家分享的是《海上繁花》《楚乔传》《白...

五个免费PDF转Word方法(附带!转换效果实测!) 推荐五个免费PDF转Word方法,助力高效办公。 市面上PDF转Word工具参差不齐,有没有即免费又好用的PDF转Word方法呢,经过不断测试,总结...

高田里穗:自律塑造完美身材,自然妆容优雅,时尚品味独特 高田里穗:从特摄剧偶像到全能艺人的华丽转身 一、星光闪耀:特摄剧到影视界的新星 特摄剧中的耀眼新星 提及高田里穗...

噩耗!著名艺术家韦伟去世,享年101岁,被誉为影视界“活化石” 【惠头条】著名艺术家韦伟去世,享年101岁,影视界“活化石”告别世界 近日,影视界传来一则噩耗,享誉国内外的...

不知火舞和春丽谁更大,困扰玩家三十年的疑问 不知道大家是否还记得上一次春丽和不知火舞联动是什么时候呢? 久远之前SNK和CAPCOM相互授权打造三款游戏,SNK这边分别打造了一款卡...
为什么韩国讨厌中国的同时,又对中国文化“巧取豪夺”? 去年11月28日,2030年世博会投票结果出炉。和全世界喜气洋洋形成鲜明对比的是,韩国人痛哭流涕甚至是破口大骂。因为韩国...

面试官:“灭”字只加一笔,是什么字? 每个人在应聘的时候都会经历面试这个过程,面试实际上对于每个应聘者来说,实际上也是一种挑战。对于刚刚毕业去找工作的人来说就更是如...

回头率爆表的微卡,长安星卡不仅高颜值,底盘动力同样在线 【卡车之家 原创】微卡在我们印象当中,大多是千篇一律的外观风格,没有什么太多特点,尤其是面对如今剧增的年轻用...

《无问西东》刘淑芬跳井:这段畸形婚姻,犯了三个错误! 文/微光之下 “我把你的杯子摔了,你宁可用自己的碗喝水也不用我的,现在我把你的碗也摔了,你会用我的杯子喝水,我的...